# LIBRERÍAS REQUERIDAS
library(factoextra) # Para el PCA
library(rlang) #
library(FactoMineR) # Para el PCA
library(vegan) # Para el PCA
library(ade4) # Para el PCA
library(corrplot) # Figuras de elipses
library(ggplot2) # Figuras de dispersión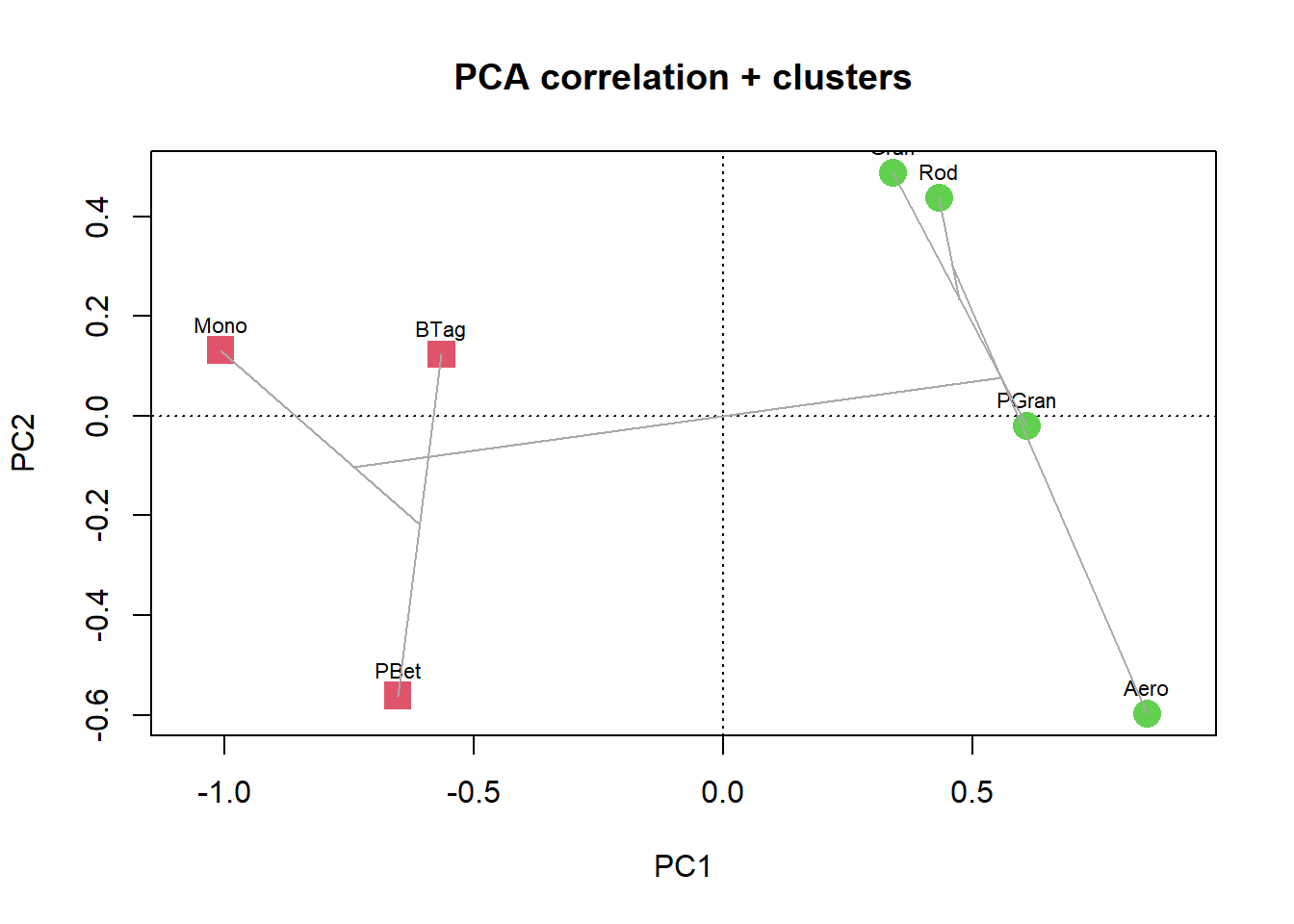
Taller 4.1 Análisis de Componentes Principales - PCA
El siguiente ejemplo relaciona a 7 lugares en playas de de Santa Marta (observaciones) y en cada una de ellas se midieron 7 variables ambientales (descriptores). En este análisis de comonentes principales - PCA, se intenta saber cuál es la relación entre variables ambientales y cómo estas estructuran o caracterizan a las localidades estudiadas. La base de datos a trabajar es FQmarino.csv.
Ejercicio tomado de: Rodríguez-Barrios (2023) Enlace del libro
Enlace de los archivos del libro
Sigatoka en cultivos de banano - Aguirre et al. (2015). Análisis de componentes principales con el paquete “dudipca” y algunas técnicas multivariadas complementarias.
PCA en factoextra - datanovia
Guía práctica sonre el PCA - datanovia
PCA para variables categóricas - R-bloggers
Capítulo PCA - Libro Numerical Ecology with R - Borcard et al. 2018
# Lectura de la base de datos "FQmarino"
datos <-read.csv2("FQmarino.csv",row.names=1) # file.choose()
View(datos)
str(datos)'data.frame': 7 obs. of 8 variables:
$ Sitio : chr "S1" "S1" "S1" "S1" ...
$ pH : num 8.42 8.49 8.51 8.56 8.61 ...
$ Cond : num 38 38.1 37.8 37.3 37.3 ...
$ Turbidez : num 1.364 0.545 1.273 1.273 0.636 ...
$ Temp : num 29.5 29.5 29.6 29.3 29.3 ...
$ Salinidad : num 2.42 2.43 2.42 2.38 2.38 ...
$ CapaFotica: num 19.7 22.1 22.1 10.8 9 ...
$ Oxigeno : num 0.097 0.147 0.331 0.17 0.098 0.098 0.098
Exploración Gráfica
# Elipses con colores
M <- cor(datos[,2:8]) # Matriz de Correlación (M)
round(head(M),2) pH Cond Turbidez Temp Salinidad CapaFotica Oxigeno
pH 1.00 -0.27 -0.04 -0.68 0.37 -0.77 -0.38
Cond -0.27 1.00 0.21 0.68 -0.19 0.61 0.12
Turbidez -0.04 0.21 1.00 0.03 -0.16 0.01 0.26
Temp -0.68 0.68 0.03 1.00 -0.03 0.97 0.59
Salinidad 0.37 -0.19 -0.16 -0.03 1.00 0.02 -0.15
CapaFotica -0.77 0.61 0.01 0.97 0.02 1.00 0.56La Figura 9.1 muestra la relación entre las variables, a partir de figuras de elipses.
x11() # Panel gráfico adicional
corrplot(M, method = "ellipse") # Figura de correlaciones con elipsesLa Figura 10.1 muestra la relación entre las variables, a partir de figuras de elipses y coeficientes de correlación de Pearson.
X11()
corrplot.mixed(M, upper="ellipse") # Figura con coeficientes de correlaciónLa Figura 11.1 otra forma de mostrar la relación entre las variables, a partir de figuras de elipses y coeficientes de correlación de Pearson.
x11()
corrplot(M, method = "circle", # Correlaciones con circulos
type = "lower", insig="blank", # Forma del panel
order = "AOE", diag = FALSE, # Ordenar por nivel de correlación
addCoef.col ="black", # Color de los coeficientes
number.cex = 0.8, # Tamaño del texto
col = COL2("RdYlBu", 200)) # Transparencia de los circulos
1) PCA con el paquete stats (pca1)
pca1 <- princomp(datos[,2:8],cor=TRUE)
1.1) Valores propios - autovalores para medir el ajuste del PCA
summary(pca1)Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 1.8454563 1.1063340 0.9919952 0.9474050 0.68078731
Proportion of Variance 0.4865298 0.1748536 0.1405792 0.1282252 0.06621019
Cumulative Proportion 0.4865298 0.6613834 0.8019626 0.9301878 0.99639798
Comp.6 Comp.7
Standard deviation 0.158789715 0
Proportion of Variance 0.003602025 0
Cumulative Proportion 1.000000000 1
1.2) Insumos del pca (names)
names(pca1)[1] "sdev" "loadings" "center" "scale" "n.obs" "scores" "call"
1.3) Valores propios - autovectores y escores
round(pca1$loadings,2) # Autoectores (loadings)
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
pH 0.43 0.42 0.18 0.61 0.20 0.45
Cond -0.36 0.16 0.74 0.27 -0.35 -0.32
Turbidez -0.65 0.62 -0.41 0.11
Temp -0.52 0.21 0.81 -0.10
Salinidad 0.13 0.67 0.60 -0.11 -0.29 -0.13 -0.26
CapaFotica -0.52 0.25 -0.13 -0.29 0.75
Oxigeno -0.35 -0.15 0.24 -0.63 0.53 -0.25 -0.22
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
SS loadings 1.003 1.006 1.010 0.992 1.003 0.994 1.002
Proportion Var 0.143 0.144 0.144 0.142 0.143 0.142 0.143
Cumulative Var 0.143 0.287 0.431 0.573 0.716 0.858 1.001round(pca1$scores,2) # Coordenadas de las localidades (Scores) Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
BTag -1.55 -0.34 0.14 0.85 -1.34 0.11 0
PBet -1.80 1.54 -0.97 0.67 0.36 -0.19 0
Mono -2.77 -0.36 0.84 -1.20 0.63 0.11 0
Gran 0.93 -1.34 -0.27 -0.96 -0.41 -0.27 0
PGran 1.67 0.05 -1.70 -0.52 0.16 0.22 0
Rod 1.19 -1.20 0.58 1.53 0.82 0.01 0
Aero 2.33 1.64 1.38 -0.36 -0.22 0.01 0
1.4) Contribución de los ejes del pca
La Figura 11.2 muestra la manera de graficar a la varinza que captura cada componente principal.
x11()
screeplot(pca1,ylab="Varianza",main="",
cex.lab=1.5, col="lightblue")
1.5) Opciones de biplot, por combinaciones de ejes.
La Figura 11.3 muestra la ordenación de las locaidades y las variables ambientales en las 7 bahías evaluadas (gráfico de biplot).
biplot(pca1,choices = 1:2, cex=0.9)
abline(v=0,lty=2, col=4)
abline(h=0,lty=2, col=4)# Otras opciones de pca por combinaciones de ejes
biplot(pca1,choices = 2:3, cex=0.9)
biplot(pca1,choices = c(1,3), cex=0.9)
2) PCA con el paquete FactoMiner
2.1) Inserción de las variables al PCA
# Insertar las variables al PCA
names(datos)[1] "Sitio" "pH" "Cond" "Turbidez" "Temp"
[6] "Salinidad" "CapaFotica" "Oxigeno" datos.PCA<-datos[, c("pH", "Cond", "Turbidez", "Temp", "Salinidad",
"CapaFotica", "Oxigeno")]
2.1) PCA con escalamiento de las variables (similar a la matriz de correlación)
# Realización del pca con la librería FactoMiner
pca2<-PCA(datos.PCA , scale.unit=TRUE, ncp=5, graph = FALSE)
2.2) Figura del PCA
La Figura 12.1 muestra la ordenación de las locaidades en las 7 bahías evaluadas (gráfico de biplot).
# Figura del pca realizado (grafica de observaciones)
plot.PCA(pca2, axes=c(1, 2), choix="ind", habillage="none", col.ind="black",
col.ind.sup="blue", col.quali="magenta",
label=c("ind", "ind.sup", "quali"))
2.3) Circulo de contribuciones de las variables
La Figura 12.2 muestra el circulo de contribuciones para identificar a las variables con mayor aporte por cada componente principal del análisis.
# Circulo de contribuciones
plot.PCA(pca2, axes=c(1, 2), choix="var", col.var="#ff0000", new.plot=T,
col.quanti.sup="blue", label=c("var", "quanti.sup"), lim.cos2.var=0)
2.4) Selección de variables a partir del PCA
# Variables con mayor aporte al PC1
dimdesc=dimdesc(pca2, axes=1:2)
round(dimdesc$Dim.1$quanti,4) correlation p.value
Temp 0.9594 0.0006
CapaFotica 0.9564 0.0007
pH -0.7899 0.0346
3) PCA con el paquete vegan
# Realización del pca
pca3 <- rda(datos[,c(2:8)], scale = TRUE)
3.1) Insumos del análisis
# Insumos del pca
summary(pca3)
Call:
rda(X = datos[, c(2:8)], scale = TRUE)
Partitioning of correlations:
Inertia Proportion
Total 7 1
Unconstrained 7 1
Eigenvalues, and their contribution to the correlations
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6
Eigenvalue 3.4057 1.2240 0.9841 0.8976 0.46347 0.025214
Proportion Explained 0.4865 0.1749 0.1406 0.1282 0.06621 0.003602
Cumulative Proportion 0.4865 0.6614 0.8020 0.9302 0.99640 1.000000
Scaling 2 for species and site scores
* Species are scaled proportional to eigenvalues
* Sites are unscaled: weighted dispersion equal on all dimensions
* General scaling constant of scores: 2.54573
Species scores
PC1 PC2 PC3 PC4 PC5 PC6
pH 0.7600 -0.05946 -0.39634 -0.16779 -0.39815 -0.03017
Cond -0.6409 0.03919 -0.15521 -0.67510 -0.17577 0.05298
Turbidez -0.1626 0.69132 -0.59117 -0.02172 0.26687 -0.01640
Temp -0.9231 -0.21981 -0.06696 -0.04433 -0.05922 -0.12436
Salinidad 0.2220 -0.71203 -0.56910 0.09845 0.18854 0.02044
CapaFotica -0.9203 -0.26095 -0.03157 0.01094 0.08801 0.04456
Oxigeno -0.6245 0.16367 -0.22590 0.57864 -0.34878 0.03860
Site scores (weighted sums of species scores)
PC1 PC2 PC3 PC4 PC5 PC6
BTag -0.8103 0.29431 -0.1336 -0.8605 1.8923 -0.68752
PBet -0.9363 -1.34295 0.9378 -0.6784 -0.5141 1.12733
Mono -1.4457 0.31382 -0.8173 1.2159 -0.8964 -0.64531
Gran 0.4866 1.16512 0.2621 0.9789 0.5863 1.60931
PGran 0.8705 -0.04719 1.6534 0.5317 -0.2280 -1.31394
Rod 0.6186 1.04517 -0.5617 -1.5570 -1.1561 -0.05927
Aero 1.2166 -1.42828 -1.3407 0.3694 0.3161 -0.03060
3.2) Autovalores
# Ajuste del pca
round((ev <- pca3$CA$eig),2) PC1 PC2 PC3 PC4 PC5 PC6
3.41 1.22 0.98 0.90 0.46 0.03
3.3) Figura del PCA
La Figura 12.3 muestra dos opciones de visualizar los resultados del pca “scaling 1” y “scaling 2”.
# Panel con dos figuras del pca
x11(12,6)
par(mfrow=c(1,2))
biplot(pca3, scaling=1, main="PCA - scaling 1")
biplot(pca3, main="PCA - scaling 2") #—
Taller en casa
Realizar el cálculo del los siguientes insumos de la página 126 a 127, del libro Análisis de datos ecológicos y ambientales: Aplicaciones con el programa R el cual se encuentra en la biblioteca.
Ajuste de los componentes principales.
Figura de atovalores
- Figura del modelo de Kaiser
- Figura del modelo de Vara Quebrada
#—
4) Análisis avanzado de PCA
Combinación de clasificación y ordenación
Tomado de 5.3.2.6 Combining Clustering and Ordination Results del libro de Borcard et al. (2018), el cual se encuentra en la base de la Biblioteca de Unimagdalena.
4.1) Generación de grupos con la distancia euclídea y el agrupamiento de Ward
str(datos) # Identificación de las variables cuantitativas'data.frame': 7 obs. of 8 variables:
$ Sitio : chr "S1" "S1" "S1" "S1" ...
$ pH : num 8.42 8.49 8.51 8.56 8.61 ...
$ Cond : num 38 38.1 37.8 37.3 37.3 ...
$ Turbidez : num 1.364 0.545 1.273 1.273 0.636 ...
$ Temp : num 29.5 29.5 29.6 29.3 29.3 ...
$ Salinidad : num 2.42 2.43 2.42 2.38 2.38 ...
$ CapaFotica: num 19.7 22.1 22.1 10.8 9 ...
$ Oxigeno : num 0.097 0.147 0.331 0.17 0.098 0.098 0.098# Generación de grupos
datos.w <- hclust(dist(scale(datos[,c(2:8)])), "ward.D")
4.2) Cortar la clasificación en 2 grupos
gr <- cutree(datos.w, k = 2)
grl <- levels(factor(gr))
4.3) Base de datos con el factor agrupador
datos.gr=data.frame(gr,datos) # Dataframe con la variable agrupadora (gr)
datos.gr$gr=as.factor(datos.gr$gr) # crear los grupos como factor
4.4) Extraer los escores de los sitios con el pca del paquete “vegan”
sit.sc1 <- scores(pca3, display = "wa", scaling = 1)
4.5) PCA con simbolos y colores por cada grupo
La Figura 13.1 muestra los dos grupos de bahías generados en el pca.
x11()
pc4 <- plot(pca3, display = "wa", scaling = 1, type = "n",
main = "PCA correlation + clusters")
abline(v = 0, lty = "dotted")
abline(h = 0, lty = "dotted")
for (i in 1:length(grl)) {
points(sit.sc1[gr == i, ],
pch = (14 + i),
cex = 2,
col = i + 1)
}
# Agregar los rótulos de los sitios
text(sit.sc1, row.names(datos), cex = 0.7, pos = 3)
# Adicionar el dendograma al pca generado (uniones entre puntos)
ordicluster(pc4, datos.w, col = "dark grey")
# Adicionar la leyenda de la figura (**Nota**: hacer clic en la figura)
legend(locator(1),
paste("Grupo", c(1:length(grl))),
pch = 14 + c(1:length(grl)),
col = 1 + c(1:length(grl)),
pt.cex = 2)
5) PCA por tipos con la función “dudi.pca” del paquete ade4
pca5 <- dudi.pca(datos[,c(2:8)],scannf=F,nf=2,scale=T)
5.1) Figuras del pca por tipo de grupo
La Figura 13.2 muestra el agrupamiento por elipses en el pca.
s.class(pca5$li,datos.gr$gr, cpoi = 2)La Figura 15.2 muestra el agrupamiento por líneas en el pca.
s.class(pca5$li,datos.gr$gr, cell = 0, cstar = 0.5)La Figura 15.3 muestra el agrupamiento por triangulos en el pca.
coul <- c("red", "blue")
s.chull(pca5$li,datos.gr$gr, cpoi = 1, col = coul)